こんにちは、データサイエンスチームの白石です。
前回は、Attention 機構を用いることで、画像分類モデルの改善ができないかを検討しました。また、Attention 機構を用いることで、画像中のどこに注目すべき領域があるのかを、モデル内に組み込めるということを示しました。
今回は、また別の角度からのアプローチとしてメトリック学習(Metric Learning)と呼ばれるテクニックについてご紹介します。代表的な手法として、Triplet Loss(※1)について紹介します。また、定義によっては Metric Learning に含めないこともあるようですが、より実装が簡易な Center Loss(※2)と呼ばれる手法も紹介します。最後に、Center Loss を実装したモデルについて訓練を行い、精度測定を行います。
メトリック学習は、類似画像検索や顔認証といったアプリケーションで使用されることの多いアプローチで、例えば、「特徴量間の距離メトリックを使用することで、サンプル間の類似性を測定する手法」などと定義されます。
以下に直感的なイメージを示します。
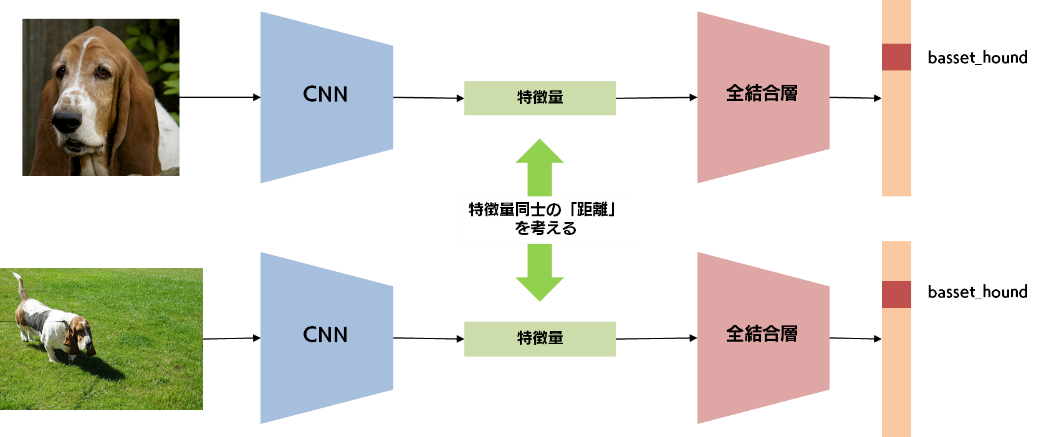
2枚の画像から、同一の CNN によって別々の特徴量が抽出されています。それらの特徴量は全結合層へ入力され、分類結果が得られます。このときに得られる2つの特徴量に対し、何らかの指標によって、その近さを測定します。このような指標を距離メトリックと呼び、例えば、ユークリッド距離などが当てはまります。この距離メトリックを用いることで、2枚の画像から得られた特徴量同士の距離が近ければ2枚の画像は類似しており、距離が遠ければ2枚の画像は類似していない、という判断を行うことができます。
さて、このように2枚の画像サンプル間の類似度を距離メトリックによって測定できると、画像分類というタスクにとって、何が嬉しいのでしょうか? ひとことで言えば、「異なるカテゴリの画像同士から得られる特徴量は遠く、同じカテゴリ同士の画像から得られる特徴量は近くする」ことができるようになります。
2枚の画像が、異なるカテゴリに属している場合について考えてみましょう。2枚の画像から得られる特徴量間の距離が近い場合は、この2枚の画像を見分けることが難しい、ということを意味します。逆に、特徴量間の距離が遠い場合は、この2枚の画像を見分けることは簡単になるので、画像分類においては理想的です。逆のパターンとして、2枚の画像が、同じカテゴリに属している場合も考えてみましょう。2枚の画像から得られる距離が近い場合は、2枚の画像は同一カテゴリに分類されやすそうです。一方で、2枚の画像から得られる距離が遠い場合は、全結合層を複雑にしない限り、2枚の画像を同一のカテゴリに分類するのは難しそうです。
このような洞察から、以下のようなペナルティを加えて CNN を訓練できると、良い特徴量を得られるであろうことが想像できます。
このような距離メトリックを用いたペナルティを損失関数として設計し、訓練を行うことをメトリック学習と呼びます。そして、そのペナルティの具体例が、Triplet Loss や Center Loss です。
Triplet Loss は、上記のペナルティを愚直に損失関数に反映させようとしたものです。
下図をご覧ください。Triplet とは「3つ組」という意味ですが、下図には、3枚の画像 \(x_{anc}, x_{pos}, x_{neg}\) が「3つ組」として登場しています。それぞれについて、どのような役割を担っているのかを説明します。まず、\(x_{anc}\) は基準(アンカー)となる画像です。次に、\(x_{pos}\) は、基準となる画像と同一のカテゴリに属している画像です。そして、\(x_{neg}\) は、基準となる画像とは異なるカテゴリに属している画像です。
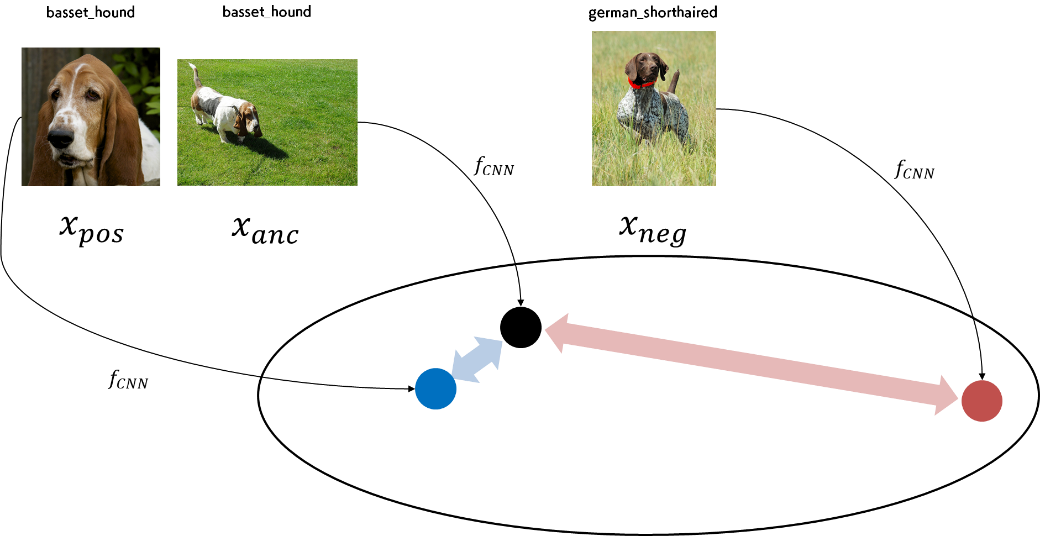
これらの画像は、\(f_{CNN}\) という関数(上図の CNN に対応します)を通じて、特徴量に変換されます。特徴量はベクトルですので、高次元の空間のある1点を表します。図中に存在する黒丸、青丸、赤丸は、それぞれその特徴量に対応する点を表し、\(f_{CNN}(x_{anc}), f_{CNN}(x_{pos}), f_{CNN}(x_{neg})\) に対応しています。黒丸と青丸が近い位置になり、黒丸と赤丸が遠い位置になるように CNN を訓練する、というのが Triplet Loss の大きな方針です。
Triplet から得られる特徴量を用いて、下式のようなペナルティを損失関数として定義することができます。
\[TripletLoss = \max(D(f_{CNN}(x_{anc}), f_{CNN}(x_{pos})) - D(f_{CNN}(x_{anc}), f_{CNN}(x_{neg})) + \alpha, 0)\]
まず、右辺の全体を確認しましょう。max によって囲まれていることにより、第1項が負の時は、損失はゼロになる、という式になっています。max の第1項では、「anc-pos 間の距離と anc-neg 間の距離という2つの距離の差」が採られ、「\((\alpha)\)」がプラスされています。
「2つの距離の差」について、詳細に確認していきましょう。3つ組である3枚の画像について、\(f_{CNN}\) によって特徴量が抽出されると、適当な距離メトリック D によって、同一カテゴリ同士での距離、異なるカテゴリ同士の距離が算出されています。もし、同一カテゴリ同士での距離が、異なるカテゴリ同士の距離よりも大きければ、「2つの距離の差」はその分だけ大きくなり、損失が発生します。しかし、異なるカテゴリ同士の距離の方が同一カテゴリ同士の距離よりも「十分に」大きい場合は、すでに適切に CNN が訓練されているとみなせるため、損失は発生してほしくありません。この時は、max の第2項である0が採用され、損失は0となります。また、異なるカテゴリ同士の距離の方が同一カテゴリ同士の距離よりも「十分に」離れている、というときの「十分に」という表現を数値化したものが、正のハイパーパラメータである \((\alpha)\) です。これによって、「2つの距離メトリックの差」が \((\alpha)\) より小さければ、仮に異なるカテゴリ同士の距離の方が大きかったとしても、損失を与えることになります。
以上のように、Triplet Loss によって、距離メトリックを用いた損失関数を定義することができました。
しかし、Triplet Loss には、「どのようにしてTriplet」を作るのか、という問題があります。訓練の最初の内は、\(x_{anc}\) をもとに、ランダムに \(x_{pos}\) と \(x_{neg}\) をサンプリングして triplet を作れば良さそうですが、訓練が進むにつれて、ほとんどの画像は適切に分類できるようになってしまうため、Triplet Loss はほとんど0になり、訓練の効率が下がってしまいます。そのため、Triplet Loss が発生するようなできるだけ「難しい triplet」を作りたい、と考えるのは自然な発想です。具体的には、\(x_{anc}\) と同一のカテゴリなのに距離が大きい画像を \(x_{pos}\) としてサンプルし、\(x_{anc}\) と異なるカテゴリなのに距離が小さい画像を \(x_{neg}\) としてサンプルしたい、ということになります。Triplet Loss を適用するためには、このような難しい triplet を作り出すための戦略(Triplet マイニング)が必要になるため、実装が煩雑になってしまうことがあります。
私はあまり調査できていないのですが、近年の研究では、適切な Triplet を高速にマイニングするような手法も提案されているようなので、興味がある方は調べてみると良いでしょう。
次に、Center Loss を紹介します。この手法は、先に示した2つのペナルティのうち、2つの画像が同一カテゴリに含まれる場合のペナルティを実現するものです。Center とは「中心」という意味ですが、この手法では、「同一カテゴリの画像から得られる特徴量の中心」を指します。
下図をご覧ください。ここに4枚の画像があり、basset_hound に属する画像が2枚、german_shorthaired に属する画像が2枚用意されています。それぞれの画像から CNN によって、大きい青い丸や大きい赤い丸に対応する特徴量が抽出されます。また、小さい青い丸や小さい赤い丸は、カテゴリごとに用意された中心(Center)です。
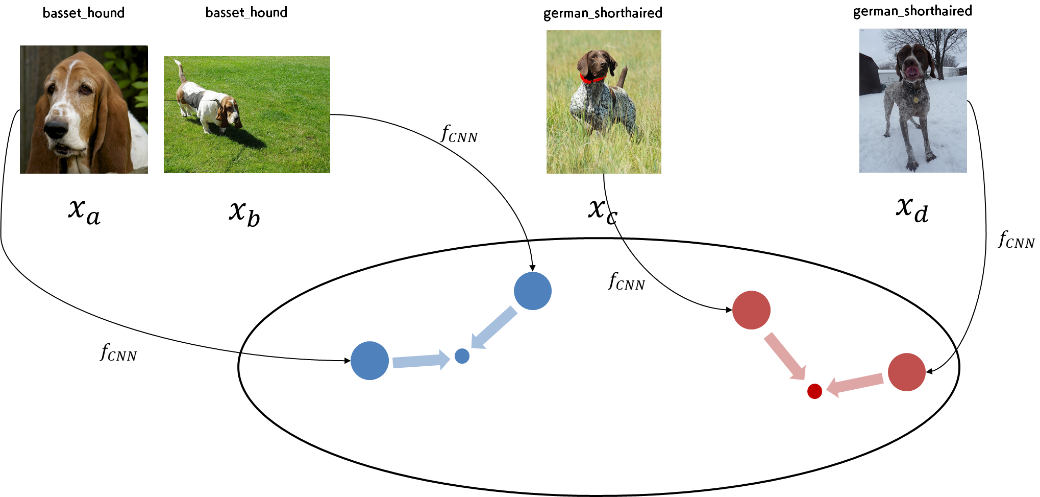
画像から得られる特徴量(大きい丸)が、カテゴリ固有の中心(小さい丸)に近づくように CNN を訓練する、というのが Center Loss の目標となります。
Center Loss は、数式では以下のように表されます。
\[CenterLoss = \frac{1}{2} \| f_{CNN}(x) - c_y \|_2^2\]
Triplet Loss と比べると、だいぶすっきりした式になっています。\(f_{CNN}(x)\) は画像 \(x\) から CNN によって抽出された特徴量を、\(c_y\) は \(x\) が属しているカテゴリ \(y\) の Center を、それぞれ表しています。そして、\(\|\cdot\|_2^2\) は、L2距離の二乗を表します。つまり、Center Loss は、\(f_{CNN}(x)\) と \(c_y\) との間の距離(の二乗)に対して課せられている損失ですので、2点の間の距離がより近くなるように促す損失になっています。この損失を加えることで、各画像の特徴量がカテゴリ固有の Center に近づいていき、結果として同一カテゴリ内の画像間の特徴量が近づくようにように CNN が訓練されます。
Center Loss の肝である \(c_y\) は、過去に得られた \(f_{CNN}(x)\) から逐次的に更新され、下式のようにどんどんその位置を変えていきます。しかし、十分に訓練が進み、多くの画像で \(f_{CNN}(x)\) と \(c_y\) との間の距離が小さくなるにつれて、比較的安定した場所にとどまるようになります。
\[\boldsymbol{c}_y \leftarrow \boldsymbol{c}_y + \beta (f(x) - \boldsymbol{c}_y)\]
Center Loss は、Triplet Loss とは異なり、異なるカテゴリの画像から得られる特徴量間の距離を大きくするような損失ではないということで、片手落ちの印象があります。実際、文献によっては、Center Loss をメトリック学習の一種とみなしていないような文献もあるようです。しかし、同一カテゴリ内限定とはいえ、特徴量間の距離メトリックをもとにした損失を課すという点で、本稿では同一の枠組みで紹介しました。
Center Loss では、効率的な Triplet をマイニングするための実装上の苦労がなく、ベースラインの手法とほとんど同じ訓練のプロセスが使いまわせるというのが利点です。
ここから、Center Loss の実装について解説していきます。今回もNotebookを用意していますので、そちらも併せてご覧ください。
Center Loss を適用するためのネットワークは、ベースラインモデルと完全に同じ構造をしています。しかし、Center Loss の計算 と Centers の更新という計算が必要になるため、簡潔な実装のためには少々工夫を加えています。
今回は、CenterLossNetwork というクラスを作成しました。その属性として、各カテゴリの中心 \(c_y\) を表す centers を設け、推論時に得られた特徴量を一時的に保持しておく、feature_を設けています。feature_は、forward メソッド内でその値が設定され、Center Loss の計算の際に呼び出されます。
class CenterLossNetwork(nn.Module):
def __init__(self, num_classes):
super().__init__()
base_model = resnet34(pretrained=True)
self.features = nn.Sequential(
*[layer for layer in base_model.children()][:-1],
nn.Conv2d(512, 512, 1, bias=False),
nn.AdaptiveAvgPool2d(1)
)
self.fc = nn.Sequential(
nn.Dropout(0.5),
nn.Linear(512, num_classes)
)
self.centers = nn.Parameter(torch.zeros(num_classes, 512), requires_grad=False)
self.num_classes = num_classes
self.feature_ = None
def forward(self, x):
feature = self.features(x)
feature = feature.view(-1, 512)
self.feature_ = feature
return self.fc(feature)
Center Loss は具体的には、MSE Loss 関数を使って実装しています。
def center_loss_func(model, feature, target):
return F.mse_loss(feature, model.centers[target])
全体的な損失関数は、通常の分類損失に Center Loss を足し合わせて定義されます。その際、バランスを決めるハイパーパラメータ \(lambda_{center}\) を使い、以下のように表現されます。 \[Loss = CELoss + \lambda_{center} CenterLoss\]
前述のとおり、CenterLossNetwork には、centers という属性を設けています。これは、カテゴリ数×特徴量次元という形状のテンソルで、各カテゴリの中心 \(c_y\) を保持しておくテンソルです。訓練開始前は、すべての値が0で初期化されています。
self.centers = nn.Parameter(torch.zeros(num_classes, 512), requires_grad=False)
train 関数の中盤で、この centers の値をミニバッチに含まれるサンプルを用いてカテゴリごとに更新していく処理が以下のように実装されています。これは、先に述べた、各カテゴリの中心位置がどんどん変わっていくということに対応しています。
feature = model.feature_.detach()
delta = torch.zeros(model.num_classes, 512).cuda()
for i in range(feature.shape[0]):
delta[target[i]] += feature[i] - model.centers[target[i]]
for t, c in zip(*torch.unique(target, return_counts=True)):
delta[t] = delta[t] / (1 + c)
model.centers += beta_center * delta
上記のように実装した CenterLossNetwork を使って、分類器を訓練しました。今回も30回ほど実験した際の平均精度とそのばらつきを算出しました。
左右にスクロールしてご覧ください。
| Validation 精度 | Test 精度 | |
|---|---|---|
| ベースライン | 91.6 | 92.1 |
| CenterLoss モデル | 9.190±0.32 | 92.45±0.28 |
明らかにベースラインを超えている、とはいかないものの、平均的には、ベースラインを上回る精度が得られました。また、Test 精度に関しては、93%の大台に到達することもありました。Validation 精度と Test 精度が双方バランスよく高精度だったモデルでは、それぞれ、92.25%、93.09%でした。
今回はメトリック学習についてご紹介しました。その代表的な手法である Triplet Loss とCenter Loss を紹介し、Center Loss については実装と実験結果を示しました。Center Loss は、前回紹介した Attention 機構を用いたような手法とは異なり、推論速度を維持したまま精度を向上させることができます。また、マルチタスク学習とは異なり、ネットワークの構造自体には手を加えないので、実装も比較的簡単に行えます。ぜひご自身でも試してみてください。
次回は、連載の最終回です。今まで行ってきたことをまとめつつ、今回の連載では詳しく説明できなかったいくつかの改善方法についてご紹介していく予定です。
それではまた次回!
(※1)Hoffer, Elad, and Nir Ailon. "Deep metric learning using triplet network." International Workshop on Similarity-Based Pattern Recognition. Springer, Cham, 2015.
(※2)Wen, Yandong, et al. "A discriminative feature learning approach for deep face recognition." European conference on computer vision. Springer, Cham, 2016.
関連ページ
深層学習入門:画像分類モデルを作ろう(1) |