こんにちは。データサイエンスチームの小松﨑です。
本記事では機械学習のモデルを作るときに非常に重要になるモデルの評価について書いてみたいと思います。昨今は AI という文字を見ない日はないほど AI の取り組みが広がっていますが、近年 AI と呼ばれるものの中身は機械学習のモデルであることが多いです。 AI と機械学習の違いなどについてはこの記事では述べませんが、機械学習のモデルを作るプロセスにおいて評価は最も重要と言っても過言ではないと思います。私自身、機械学習プロジェクトでは真っ先に評価方法を明確にし、評価用データセットを整備するようにしています。何故なら自分ではどんなに素晴らしいものを作ったと思っていても、それをお客様にしっかりと理解し納得してもらう必要があるからです。
評価といっても課題やアルゴリズムの種類によって様々なものがありますが、本記事では基本的なケースとして、例えば出来上がった製品に異常があるかないかを予測するような、いわゆる 2 値分類に相当する場合の評価について考えてみたいと思います。

本章では、評価と聞いて多くの人が、おそらく思い浮かべる言葉である「精度」について考えます。
評価と聞いて多くの人がまず思い浮かべる言葉は精度ではないでしょうか。精度 90% を達成した、などと使われます。精度とは何でしょうか。精度 90% であれば、何かしら予測を 10 回実施したときに 9 回正解したことを意味します。非常に分かり易く、それで説明が十分な場合もあるでしょう。しかしそれだけでは不十分で、誤解を与えたりすることもあります。例えば製品の異常を検知したい場合を考えてみましょう。正常な製品のデータは集めるのが簡単であるのに対し、異常な製品についてはデータを集めるのが難しい場合があります。そのため、評価用に用意したデータセットには正常データが 90 個に対し、異常データは 10 個しか含まれていないとします。極端な例ですが、この場合全て正常と予測した場合、精度は 90% となります。計算上は正しいですが、 90% と聞いてイメージする良いモデルではないことがわかるかと思います。これでは精度という指標では意味を持ちませんね。別の例として、評価用データセットに正常データを 50 個、異常データを 50 個 のように同数程度含む場合を考えます。この場合、全て正常と予測するようなモデルでは精度は 50% と低くなるため、精度という評価指標でもある程度適切な評価ができると考えられます。
極端な例で精度を評価指標として用いた場合の欠点を述べましたが、実際の機械学習モデル構築のプロセスにおいては精度を使用することはほとんどありません。その大きな理由は、異常検知を例にとると精度という指標は、正しく正常を予測できた場合と、正しく異常を予測できた場合を混ぜて評価してしまうものだからです。モデルが正常と異常のどちらを間違いやすい傾向があるかなど、より詳細な情報がつぶれてしまいます。そのため、正常と予測した場合と、異常と予測した場合は分けて集計する方がよいでしょう。その観点で話を続けます。

本章では、機械学習モデルの評価において便利な「混同行列」について説明します。
単純な異常検知の場合、正解は正常と異常の 2 パターン、予測結果も同様に 2 パターンになります。すなわち下図のように 2×2 の表を作ることで、情報を漏れなく表現することができます。このように正解と予測結果を対応させた表を混同行列 (confusion matrix) と呼びます。下図の混同行列では、異常を Positive 、正常を Negative としていることにご注意ください。正常を Positive としたい気もしますが、異常検知のタスクでは「異常を検知する」ことに着目するため、異常である場合を Positive とします。このように正解も予測結果も、異常や正常などの情報 (機械学習用語ではラベルと呼びます) を Positive (陽性) と Negative (陰性) で表します。そして予測結果が正解である場合、頭に True (真) を付け、不正解の場合は頭に False (偽) を付けます。慣れていないと混乱しますが、図を見ながら少し頭を整理してみてください。また今後の説明のために、図に記載のように、例えば True Positive を TP のように略して記載する場合があります。
なお、ここで紹介する混同行列はサイズが 2×2 ですが、正解と予測の種類が正常と異常の2 値より多い場合、例えば 10 種類の部品の画像を分類するモデルなどの場合には、混同行列のサイズは 10×10 などとタスクに合わせて変える必要があります。
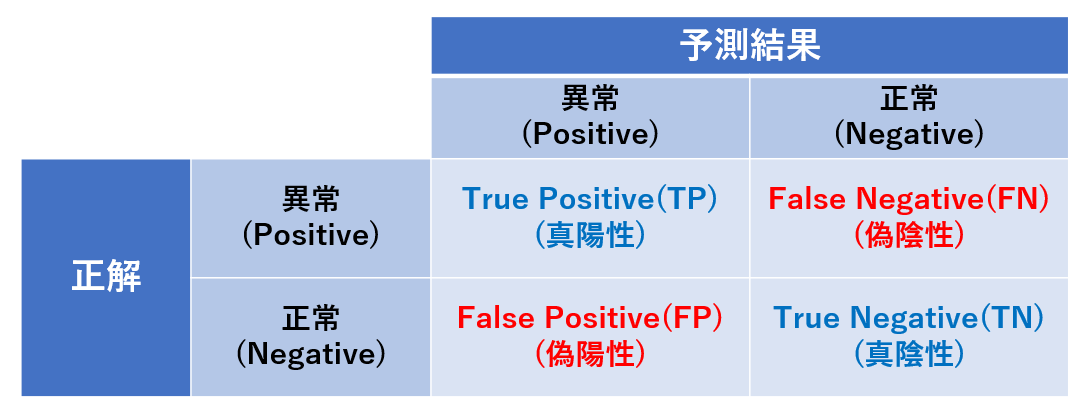
本章では、混同行列を用いて計算される評価指標について説明します。念のために言及しておきますが、混同行列を実際に使用する場合、 TP などには予測結果の数を数え上げた整数値が入ります。例えば Positive と予測して正解した数が 10 回である場合 TP には 10 が入ります。
本記事の最初の方に説明した精度は、より正確な意味を捉えるために正解率 (Accuracy) と呼ばれる場合があり、次の式で計算します。
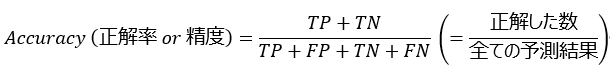
分母には混同行列の全ての要素が含まれています。意味はわかりやすいですが詳細な情報をそぎ落としてモデルの性能を1つの指標で表しており、取扱いに注意が必要です。
次に説明するのは、異常(正常)をどれだけ正しく異常(正常)と予測できたか、という「網羅性の観点」を表す指標になります。例えば異常データが 10 個あり、 7 個は正しく異常と予測し、 3 個は正常と予測した場合、 70% を正しく予測できたことになります。このように、正解をどの程度網羅して検出することができたか、ということに着目する指標について考えます。本記事では異常を Positive と呼んでおり、正解が Positive であるデータのうち、正しく Positive と予測できたデータの割合を True Positive Rate (真陽性率 TPR) と呼びます。またこれを Recall(再現率)と呼ぶこともあり、後にもう少し詳細な使い方について説明するときに呼び分けをしますが、今は頭の片隅におく程度で問題ありません。
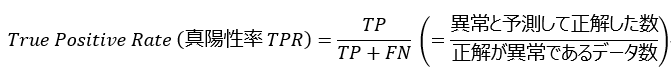
TPR は正解が Positive である場合のものです。一方、正解が Negative のデータについては、どれだけ Negative を予測できたかではなく、どれだけ Negative を間違えて Positive と予測してしまったか、と表現する場合が一般的です。混同行列内の言葉で言い換えると、 TN ではなく FP を使うことになります。この割合を False Positive Rate (偽陽性率 FPR)と呼び次のように計算します。
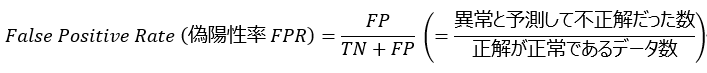
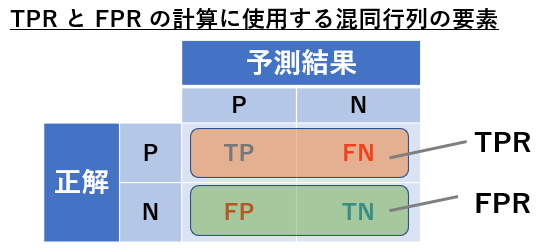
わかりやすさのために、混同行列のどの要素を TPR と FPR の計算で使用しているかについて、下図に示します。使われている要素を枠で囲っています。上式の定義から TPR も FPR も 0 から 1 の間の値をとり、 TPR は大きいほど良く、 FPR は小さいほど良い結果であることを意味します。
ここまで紹介した「網羅性の観点」に対して「予測結果がどの程度正確かという観点」も重要です。例えば Positive(異常)と予測した結果が 10 個あり、その中で 6 個が正解だったとした場合、 Positive に関する予測結果は 60% 正しかったことになります。このような評価指標は Precision(適合率)と呼ばれ次のように計算します。
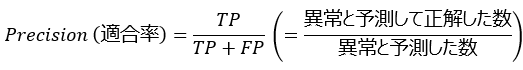
予測結果の正解の割合であるため、 Accuracy(正解率)との違いで混乱することがあるかもしれませんが、 Accuracy は Positive も Negative も含めた全ての予測結果を含む指標に対して、 Precision は Positive と予測した結果のみ含むことにご注意ください。
本章では混同行列から計算する評価指標について「網羅性」と「予測結果の正確性」の 2 つの観点から紹介しました。混同行列から計算される指標は他にもありますが、混乱を避けるためと、本記事での説明方針から指標の紹介はここまでとします。
本章での説明により、精度よりも予測結果をより詳細に表現可能な評価指標について理解できたかと思います。これらの指標を使うことで予測結果について定量的な評価ができますが、実は機械学習モデルを評価するという観点からはこれでもまだ不十分な場合があります。ここで言う機械学習モデルの評価とは、例えば複数のモデルがある場合に、より優れているモデルがどれか判定することを意味します。そのためにどのように考えればよいかについて、以降説明を進めていきます。
この章では一旦評価指標から離れて、 Positive(異常)と Negative(正常)の予測をどのように行うかについて簡単に説明します。結論からいうと、機械学習モデルが出力する「分類スコア」に基づいて予測を行うことになります。
分類スコアとは一般的な用語ではなく様々な呼び方をされていると思いますが、本記事で意味を理解すれば他の場面でも混乱することはあまりないと思います。一般的に統一された呼び方がないようなので、本記事ではそのように呼ぶこととします。分類スコアの出力方法などについての詳細は割愛しますが、機械学習モデルの多くは分類スコアを出力するとご理解ください。
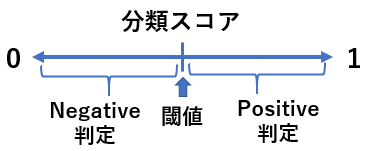
分類スコアは 0 から 1 の間をとる値です。異常検知などで Positive(異常)と Negative(正常)を予測する 2 値分類の場合、分類スコアが大きく 1 に近いほど Positive の可能性が高く、値が小さく 0 に近いほど Negative の可能性が高いとモデルが判断していることを意味します。この説明を聞くと、分類スコアは確率に似ていると感じるかもしれません。シーンによっては確率と同一視できない場合もありますが、おおよそそのように理解して良いと思います。 Positive と Negative を判定するために、分類スコアに閾値を設定する必要がありますが、それは基本的に人が設定する必要があります。

分類スコアの閾値はどのように設定すればよいでしょうか。これは何を重要視するかによって変わります。引き続き異常検知を例にします。例えば異常 (Positive) をできるだけ見逃したくない場合、少しでも怪しい場合には異常と判定するでしょう。分類スコアで話をすると、少しでも怪しい、というのは例えば分類スコアが 0.3 などと低い場合でも異常と判定することを意味します。この場合、分類スコアの閾値は低く設定します。一方、予測結果についてできるだけ誤検知を減らしたい場合には、異常であると強く確信する場合のみに異常と判定するでしょう。その場合は分類スコアの閾値を高く設定します。
前章で分類スコアの考え方を紹介し、閾値の設定の仕方によって予測結果 (Positive or Negative) が変わることを説明しました。これは分類スコアの閾値によって混同行列の結果が変化することを意味します。本章では、分類スコアの閾値を変化させたときの混同行列の変化について考察します。
例えば分類スコアの閾値を 0.5 としている場合に、正解が Positive で予測結果も Positive となった数、すなわち TP の値が 10 であったとします。このとき同時に FP の値が 10 と仮定しましょう。もし分類スコアの閾値を 0.8 に上げたら TP と FP はどのように変化するでしょうか。閾値を上げるとは、より判断を厳しくし、より強く Positive であると確信したときのみ Positive と判定することを意味します。この場合、まずは間違いが減少することが期待できると思います。そのため間違って Positive と予測した数である FP の値は元の 10 より小さくなる可能性があります。一方で 正しく Positive と予測できた数である TP の値はどうなるでしょうか。正しく予測できた予測結果の中には、分類スコアが閾値 0.5 を少し超えた 0.55 のものが含まれているとします。その場合、閾値を 0.8 とすることでその予測結果は Negative に変わり、正しく Positive と予測しないことになります。このように考えると、分類スコアの閾値を大きくすると TP の値は小さくなる可能性があります。ここまでの話をまとめると、分類スコアの閾値を大きくすれば TP と FP 共に小さくなると考えられます。
このように分類スコアの閾値は予測結果に影響するため、混同行列から計算される評価指標にも影響します。前章で説明したように、分類スコアの閾値は、見逃しの少なさや予測の正確さなど、何を重要視するかによって変更します。それでは複数の機械学習モデルがある場合に、分類スコアの閾値をどの値に設定してモデル性能の比較を実施すればよいでしょうか。

前章の問題提起を受けて、本章では、分類スコアの閾値を変化させて行う機械学習モデルの評価方法について説明します。その代表的なものの 1 つである ROC 曲線について、具体例を用いて解説します。
分類スコアの閾値によって混同行列から計算される評価指標の値が変わってしまうのであれば、閾値によらない評価をする必要があると考えられます。その 1 つのアイデアとして、閾値を 0 から 1 まで動かしながら総合的な評価をする、というものがあります。前章では閾値を変化させた場合の TP と FP の変化について考えました。しかし TP や FP はデータの数によって取り得る値の範囲が変化してしまうので、値の範囲が 0 から 1 の間に定まっている TPR と FPR に置き換えて考えた方が見通しが良さそうです。前章での考察を参考にすると、分類スコアの閾値を大きくすると TPR も FPR も共に小さくなり、閾値を小さくすると大きくなると考えられます。TPR を縦軸に、FPR を横軸にとり、分類スコアの閾値を変化させながら TPR と FPR の散布図を描くことで得られる曲線を ROC 曲線 (Receiver Operating Characteristic curve) と呼びます。この曲線は分類スコアの閾値を全ての範囲に変化させながら描くものなので、混同行列よりもより汎用的なモデルの評価に使えると考えられます。
ここからは実際にデータを用いて機械学習モデルの学習と評価を行い、 ROC 曲線を描いてみたいと思います。画像の機械学習分野で非常に有名な CIFAR-10 というデータセットを使用します。 CIFAR-10 は飛行機や自動車、鳥など 10 種類のカテゴリの写真で構成されたデータセットです。カテゴリ毎に学習データ用として 5,000 枚、評価データ用として 1,000 枚の画像が含まれます。ここまで Positive と Negative の 2 値分類について説明してきましたので、このデータセットから飛行機と自動車の 2 つのカテゴリのみを抜き出し、飛行機を Positive 、自動車を Negative とした 2値分類のモデルを構築することにします。そのため学習用データは 10,000 枚、評価用データは 2,000 枚となります。例として、飛行機と自動車のカテゴリから 4 枚ずつ抜き出した画像を下図に示します。
【参照 : CIFAR-10 データセット】
>
https://www.cs.toronto.edu/~kriz/cifar.html

本記事の本題ではありませんが、使用した機械学習モデルについて少しだけ触れておきます。画像分野の機械学習では Convolutional Neural Network (CNN) と呼ばれる画像処理に特化した深層学習 (Deep Learning) モデルを使用することが主流であり、様々なタスクで非常に高い性能を獲得しています。本記事では、そのようなモデルを使用すると性能が良すぎるあまり、主題であるROC曲線の説明に用いるには不向きなグラフとなってしまうため、あえて性能を落とすように、隠れ層がノード数 100 の 1 層のみの全結合層で構成される非常にシンプルなモデルとしました。言葉の意味などについては本記事では説明しませんので、興味のある方は調べてみてください。
評価用データに対する予測結果から得られた ROC 曲線を以下に示します。繰り返しになりますが、 ROC 曲線は分類スコアの閾値を 0 から 1 まで変化させながら TPR と FPR の対応を描いたものです。
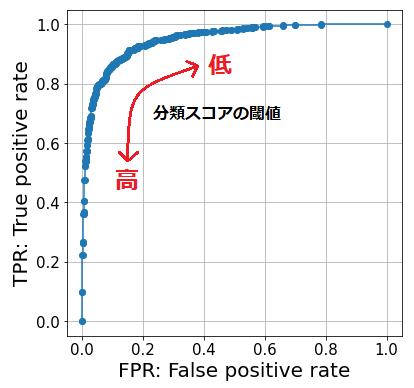
性能の高いモデルの ROC 曲線はどのようなものになるでしょうか。良いモデルは TPR が高く FPR は低くなるでしょう。 ROC 曲線では、TPR が高く FPR が低い点はより左上側にプロットされます。すなわち、良いモデルの ROC 曲線はより左上に尖ったものになります。この性質を利用することでモデル性能を比較することができます。
本章では ROC 曲線と双璧をなして活用されることの多い PR 曲線について、具体例を用いて説明します。 ROC 曲線と PR 曲線の使い分けについても解説します。
ROC 曲線の他によく用いられるものとして PR 曲線があります。 PR は Precision と Recall を表しており、 ROC 曲線と同様に、分類スコアの閾値を変化させながら Precision と Recall の関係を描くものになります。 Precision と Recall (TPR と同じ) の定義については前の説明を確認してください。 ROC 曲線との違いは、 FPR の代わりに Precision が使われていることです。 ROC 曲線と PR 曲線それぞれで使用している評価指標について、混同行列のどの要素が使われているかを下図に示します。使われている要素を枠で囲っています。
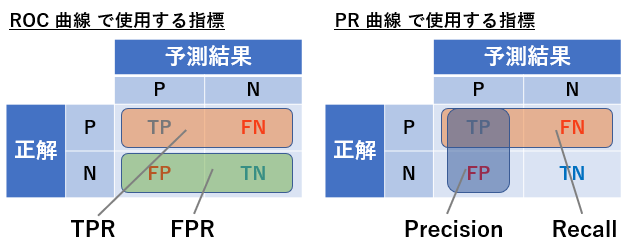
この図から TN が使われているかが、 ROC 曲線と PR 曲線の大きな違いであることがわかります。 ROC 曲線では TN も使うことで正解が Positive であるデータと Negative であるデータを平等に扱いますが、 PR 曲線は TN の値を考慮していないことから、正解が Positive のデータにより着目していると考えられます。
これらはどのように使い分ければよいでしょうか。言葉で説明しても伝わりづらいと思いますので、実際に数字を使って考えてみます。下図のように 2 つのケースを仮定し比較してみます。正解が Positive である数は両者とも 100 個とし、正解が Negative である数が左側では 100 個、右側では 900 個とします。つまり、 Positive と Negative が同数程度ある場合と、数が極端に異なる場合を考えています。それぞれ予測モデルを作成して下図のような混同行列が得られていると仮定し、そこから計算した ROC 曲線と PR 曲線に使われる評価指標の値を記載しています。
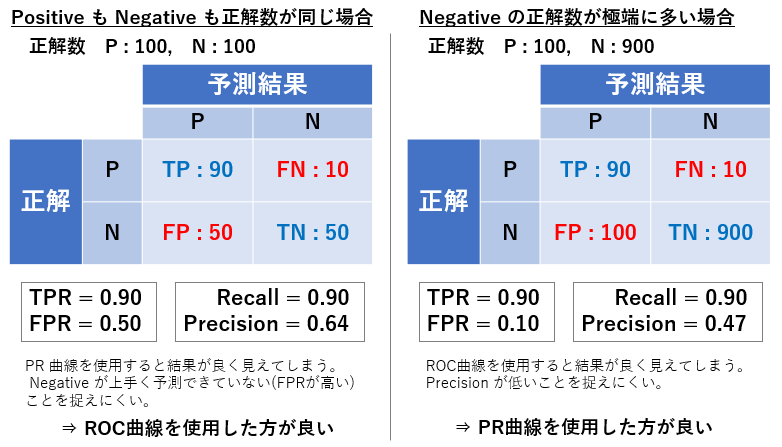
左の予測結果についてみてみると、正解が Negative であるデータについて、予測結果が Positive と Negative の同数となっています。これは正解が Negative であるデータについて完全にランダムな予測を行っている場合と同等な結果であり、つまり、 Negative データを予測する性能が低いことを意味しています。評価指標として ROC 曲線に用いる評価指標を使用する場合、FPR の値は 0.5 となり Negative データの予測性能の低さを捉えることができています。一方 PR 曲線に使われる指標を使用する場合、 Negative データに関する予測結果が含まれる Precision は 0.64 と計算され、ランダムな予測(予測性能が全くないモデルの予測)より良い結果となっています。これは前述したように TN が計算に含まれないためであり、このケースのように Positive と Negative のデータが同数程度である場合は ROC 曲線を活用した方が、より適切に評価できる可能性があります。
それでは Negative の正解数が極端に多い右側の場合はどうでしょうか。予測結果が Positive であるデータの内、正解が Negative であるデータの方が多く、Precision が 0.47 と低くなっています。一方で Recall は 0.9 と高いことから、 Negative データの一部が Positive に似ていることで誤検知が増えている可能性がありそうです。本題からは少し離れますが、 Positive に似ている Negative データを追加して再学習すると性能が改善するかもしれません。 PR 曲線に使われる指標を使うとこのような考察ができますが、 ROC 曲線の指標を使った場合はどうでしょうか。 TRP は 0.9、 FPR は 0.1 と良い値となっており、このモデルの課題が読み取りづらいと思われます。よって、このように正解データ数に偏りがある場合は、 PR 曲線を使用した方が適切な評価ができる可能性があります。
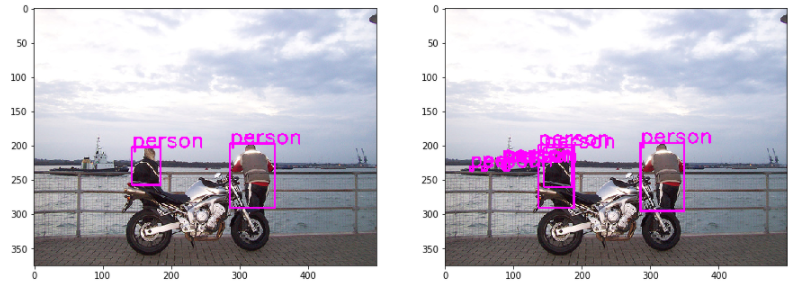
Positive と Negative の正解数が同程度の場合の具体例として CIFAR-10 データセットを使用した 2 値分類のケースを紹介し ROC 曲線を描きました。それでは Negative が極端に多い場合の例としてはどのようなものがあるでしょうか。ここでは物体検知と呼ばれるタスクの例を紹介しようと思います。物体検知とは下図のように画像中に含まれる物体の位置をバウンディングボックス (bounding box) と呼ばれる矩形として検出し、同時にその種類(この例では人 (person))を予測するタスクです。下図の例、およびこの後の検証に用いたデータは、物体検知を含む画像認識タスクにおいて有名な Pascal VOC データセットから抜粋したものになります。
【参照 : Pascal VOC データセット】
http://host.robots.ox.ac.uk/pascal/VOC/

物体検知はタスクの性質として正解データのみが与えられています。これまで考えてきた Positive と Negative の 2 値分類のように不正解 (Negative) データがありません。しかし、画像に対して予測を実施した後には、下図のように(左が正解で右が予測結果)人ではない箇所を人として誤検知する場合があります。結果としてその誤検知データを混同行列における Negative データのように扱うことができます。具体的に言うとこのような誤検知は FP となります。また物体検知モデルも分類スコアを出力しており、モデルによる予測の後処理として、分類スコアの値が閾値を下回る予測結果について最終的な結果としては出力しない仕組みとしています。そのため、分類スコアの閾値を下回り、最終的に出力されないデータは、混同行列上では Negative を正しく Negative と予測できた場合に相当し、 TN に相当すると考えることができます。一方で、検出対象を検出できずに見逃した場合は FP となります。
このように物体検知では、データセットとしては正解データしか与えられないものの、予測を行うことで混同行列の各要素に対応するデータが作られることになります。そして物体検知モデルは、一般的に分類スコアが低い予測結果 (TN に相当) を大量に出力するため、結果として混同行列上では Negative の数が相対的に多いデータセットに類似した状況になります。そのため PR 曲線で評価するのが適していると考えられます。またかなりややこしい話をしてしまいましたが、物体検知の場合は元々正解データしかないため、単純に正解データ (Positive) により着目した評価指標である PR 曲線を使うと考えてもよいかもしれません。
それでは実際に物体検知を実施した結果を使用して PR 曲線を描いてみます。予測対象とする画像は2012 年の Pascal VOC データセットから、正解として人 (person) が含まれる評価用として提供されているものを抜粋して使用しました。画像の枚数は 2,232 枚で、正解として含まれる人の数は 5,110 人となります。物体検知のモデルは新規に作成せず、 pytorch が提供している学習済モデルである Faster R-CNN ResNet-50 FPN をそのまま使用しました。分類スコアによる選別前の全予測結果として 17,962 個の予測結果を得ました。
【参照 : pytorch が提供する学習済モデル】
https://pytorch.org/vision/stable/models.html#object-detection-instance-segmentation-and-person-keypoint-detection
予測結果から作成した PR 曲線を以下に示します。 Precision が高いほど Recall が低くなるようなトレードオフの関係になっていることがわかります。今回の結果では、分類スコアに閾値を設定しない場合、言い換えれば閾値を 0 とした場合でも、 Recall の値は 1 に届いていません。また分類スコアの閾値を最大 0.98 まで大きくしましたが、 Precision も 1 に届きませんでした。物体検知のように、正解のみ与えられた場合にはこのような結果になることが一般的です。
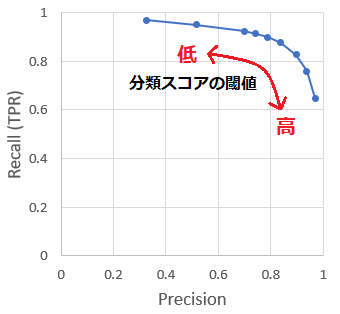
性能の高いモデルの PR 曲線はどのようになるでしょうか。 Precision と Recall はトレードオフの関係になりますが、良いモデル程、同時に高い値を実現できると考えられます。すなわち、良いモデルの PR 曲線はより右上に尖ったものになります。この性質を利用することでモデルの性能を比較することができます。
本記事では、機械学習モデルの評価方法について、最も基本的な指標である精度から出発し、 ROC 曲線と PR 曲線の使い方まで順を追って説明しました。機械学習のモデルを構築する上で非常に重要となる評価の方法についてイメージを掴んでいただければ幸いです。
当社では AI や機械学習を活用するための支援を行っております。持っているデータを活用したい、AI を使ってみたいけど何をすればよいかわからない、やりたいことのイメージはあるけれどどのようなデータを取得すればよいか判断できないなど、データ活用に関することであればまず一度ご相談ください。一緒に何をするべきか検討するところからサポート致します。データは種類も様々で解決したい課題も様々ですが、イメージの一助として AI が活用できる可能性のあるケースを以下に挙げてみます。
上記は一例となりますがデータ活用に関して何かしらの課題を感じておりましたら、当社までお気軽にお問い合わせください。
関連ページ |