こんにちは。データサイエンスチームの小松﨑です。
本記事ではデータ分析で使われる数学についてお話したいと思います。数学と言っても様々ですが、今回は線形代数と言われる分野に含まれる「行列」について書いてみます。高校で学習した人でも「聞いたことがあるけど、よくわからなかったし、何の役に立つのかもわからないな」という感想をお持ちの方も多いでしょう。微分や積分、三角関数などもそうかもしれませんね。本記事を読むことで、行列がどのように使われて役に立つか少しでもイメージを掴んで頂き、データ分析に興味をもってもらえれば幸いです。

本章では行列の役割について概要を説明します。行列には大きく以下2つの活用方法があります。
1つ目は、沢山の足し算と掛け算をすっきりとした表現で記載することができることと、行列計算に特化したアルゴリズムを使うことで効率的な計算が実施できることです。昨今 AI と呼ばれる技術の中身は深層学習 (ディープラーニング)を使っていることが多いですが、中では途方もない数の足し算や掛け算が行われています。行列を使うことでこれらの計算をシンプルにすっきりと表現することができ、行列専用のアルゴリズムで高速に計算ができます。下図に変数 x と y を共通に含む3つの式について、行列で表現した例を記載します。
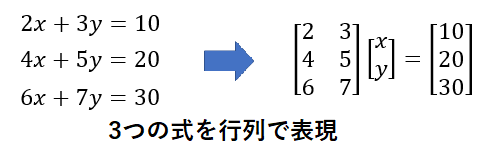
行列の計算方法については次章で簡単に説明しますが、ここでは x や y を何度も書かずに数字を行列内に列挙することでシンプルになっている、程度に認識頂ければと思います。行列専用の計算アルゴリズムについては本記事では説明しませんが、例えば機械学習の実装で使われるプログラミング言語の Python には NumPy という行列計算を高速に実施可能なライブラリが提供されています。
抽象的な話ですが、行列を使うとデータに含まれる重要な情報を取り出すことができる場合があります。本記事では特にこちらについて分かり易く解説することを目標としています。一言で言えば「あるデータ空間において、情報を沢山持つ方向を見つけることができる」と表現できます。この時点では意味が伝わらないと思いますが、本記事を読むことでこの意味を理解できるようになることを目指します。
それでは基本的なことから始めていきたいと思います。本章ではベクトルと行列について説明します。
例えば2次元の場合、ベクトルは下図のように x と y の数字を2つ並べて表現します。説明は不要かと思いますが、2次元とは縦と横のように2つの方向しかない状態のことであり、 x が1次元目、 y が2次元目に対応します。
ここでは数字を縦に並べていますが、横に並べる場合もあります。両者は区別されますが、しばらくは縦に並べたものをベクトルと呼ぶことにします。

上の例で示したベクトルを可視化してみます。矢印と点の2つの方法で表現してみました。
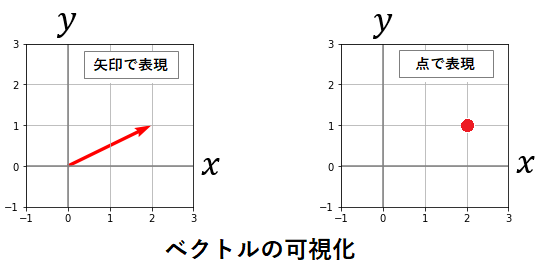
矢印はその「方向」と共に「長さ」を持ちます。矢印を描くと、いかにも「方向」という感じがしますが、同じベクトルでも点で表すと「位置 (座標) 」という感じがしないでしょうか。データ分析においては、ベクトルの「方向」に意味がある場合と「位置 (座標) 」が重要な場合があるため、文脈においてのベクトルの意味を認識することが大切です。
ベクトルの方向が重要である場合、話をわかりやすくしたり、計算を簡単にしたりするために、ベクトルの長さを1に変換することがあります。上図の例のベクトルについて、方向が重要な場合は下図のように長さ1のベクトルを使います。ベクトルの長さの計算方法については解説しませんが、気になる方は検索してみて下さい。

行列は縦方向 (行) と横方向 (列) に数字を並べた四角い形をしています。その大きさはやりたいことによって様々ですが、例として3行2列の行列を以下に記載します。
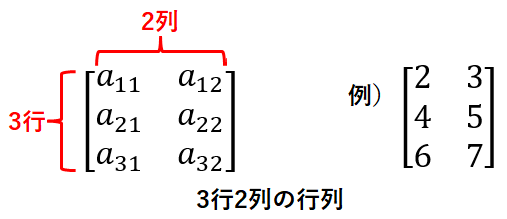
上図のように、行列の各要素について行番号と列番号の添え字で表現する場合があります。
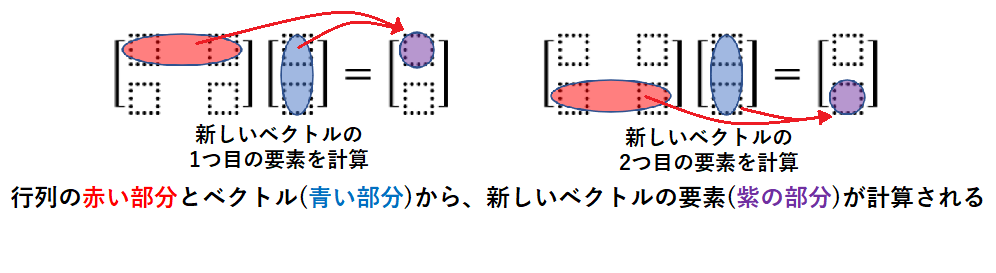
ベクトルと行列の「掛け算」が定義されています。通常の掛け算を「積」と呼ぶように「ベクトルと行列の積」と呼ばれています。2次元のベクトルと2行2列の行列との積の計算を見てみましょう。下図において、左辺がベクトルと行列の積を表しており、その結果として右辺に新しく2次元のベクトルが作られます。
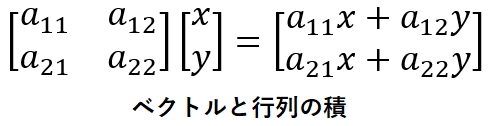
上図から計算の法則を読み取れるでしょうか。視覚的にわかりやすく表現すると下図のようになります。行列の各行を抜き出して、ベクトルと要素ごとに掛け合わせ、最後に合計することで新しいベクトルの要素を求めています。図からわかるように、積をとるベクトルの次元数と、行列の列数は同じである必要があります。ここでは2次元のベクトルと、2行2列 の行列の積の例を見ましたが、行列やベクトルのサイズが異なっても法則は全く同じです。詳細は述べませんが、行列と行列の積も同様に考えます。
具体的な計算例を見てみましょう。

この例のように、行数と列数が等しい行列を正方行列と呼びます。正方行列の場合、計算の前後でベクトルの次元数は変化しません。これは行列との積によって、ベクトルが、同じ次元数の別のベクトルに変換された、と考えることができます。上の計算前後のベクトルを可視化すると次のようになります。
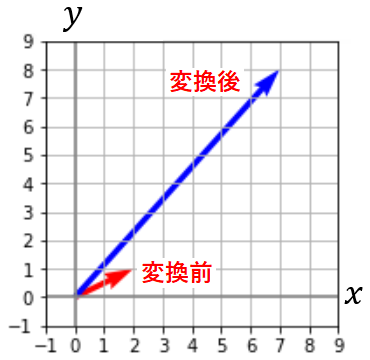
行列はベクトルを別のベクトルに変換する、という考え方はとても重要です。行列の使い方の一つの側面となります。このあたりから、行列が膨大な計算をすっきりと表現するだけの道具ではない話に入っていきます。
前章で、正方行列によってベクトルが同じ次元数の別のベクトルに変換されることを説明しました。本章では、行列にとっての特別なベクトルの話をします。
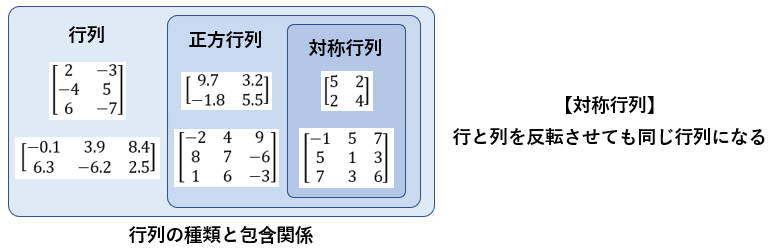
本記事の趣旨から、これ以降の話では、正方行列に限定して話を進めようと思います。さらに正方行列の中でも、データから重要な情報を取り出す観点で、特に有用である対称行列に絞って説明していきます。対称行列は、行と列を入れ替えても同一になる行列を指します。対称行列の詳しい特性などについては少し高度な話となるため割愛しますが、本記事では特に気にしなくても問題ありません。下図に対称行列を含む行列の包含関係と例を示します。
それでは本題を続けていきましょう。以下の行列 (対称行列) とベクトルについて考えます。今後扱いやすいように、それぞれ M と v 1と名前を付けています。
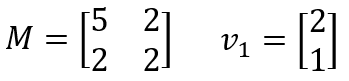
行列 M でベクトル v 1を変換してみましょう。今後は上記の名前を使って、ベクトルと行列の積を次のように表現することにします。
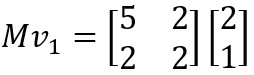
計算を進めます。
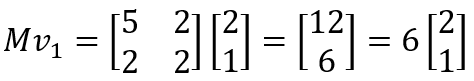
変換後のベクトルとして、変換前のベクトルと同じものが出てきました。変換前のベクトル v 1が6倍されています。つまり次のように書けます。
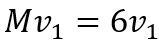
前章では、行列によってベクトルが別の方向を向いたベクトルに変換される例をみましたが、このように行列での変換によって、方向が変わらないベクトルが存在する場合があります。方向の変わらないベクトルをその行列の「固有ベクトル」と呼びます。また変換後のベクトルが変換前のベクトルの何倍になるかを表す値 (上式の場合は6) を「固有値」と呼びます。
行列 M の場合、以下のベクトル v 2も固有ベクトルであり、固有値は1です。固有値が1である場合、行列の積によってベクトルが変化しないことを意味します。
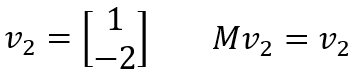
ベクトル v 1と v 2について、行列 M による変換前後を描いてみましょう。ベクトル v 2は固有値1のため変換前後で変わりませんが、わかりやすさのために少しずらして表示しています。
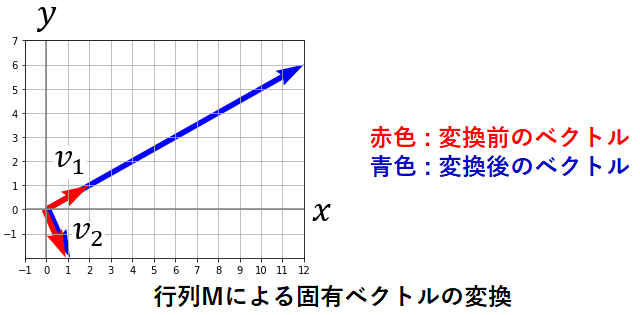
M 以外の別の行列では、別の固有ベクトルが存在するでしょう。そしてそれは上図とは別の方向を向いていると思われます。つまり固有ベクトルの方向は、その行列にとって特別な方向であり、行列の何らかの性質を表していると考えられます。この性質について考えていきたいと思います。
固有ベクトルが表す方向の意味について考える前に、少し脱線しますが固有ベクトルの便利な使い方の例について触れたいと思います。先を急ぎたい方は本章を読み飛ばしても構いません。
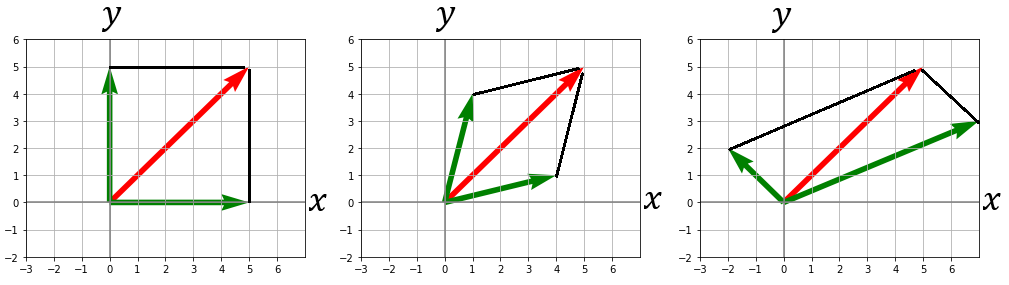
1つのベクトルを2つのベクトルの足し算で表すことを考えます。1つのベクトルは、そのベクトルを対角線とする平行四辺形の2つの辺をベクトルと見なした場合、それら2つのベクトルを足したものとして表すことができます。言葉ではわかりづらいかもしれませんが、下図の例を見ると理解しやすいかと思います。3つの赤色のベクトルはいずれも同一のベクトルを表していますが、それぞれを別の3組の緑色のベクトルの足し算として表現できます。黒線は平行四辺形を表現するための補助線です。この性質を利用して、行列の計算を楽にすることを考えてみましょう。
任意の1つのベクトル v を、以下の行列 M で変換することを考えます。この M は既に本記事で登場したものです。M の固有ベクトル v 1と v 2、およびそれぞれの固有値も再度記載します。
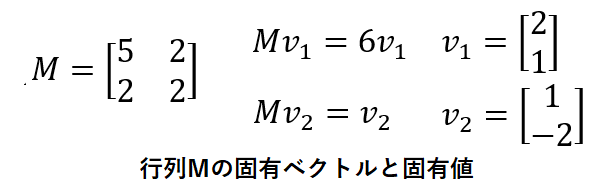
ベクトル v を M の固有ベクトル v 1と v 2の足し算で表現することを考えます。ベクトル v を対角線に持つ平行四辺形の2つの辺をベクトル v 1と v 2で表すことができればよいですが、v 1と v 2の長さを調整する必要があるでしょう。それぞれのベクトルを a 倍と b 倍することでちょうど辺の長さに等しくなるとすると、ベクトル v は次のように書くことができます。
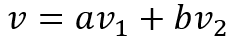
v 1とv 2で表現したベクトル v を図示すると次のようになります。V 2と bv 2の向きが逆ですが、 b が負の値となっていることを意味します。
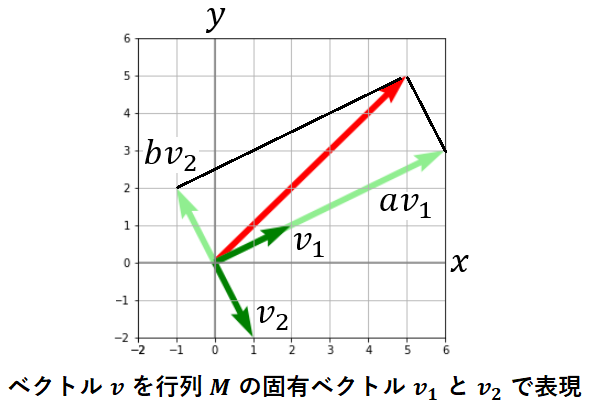
それではこのベクトル v を行列 M で変換してみましょう。
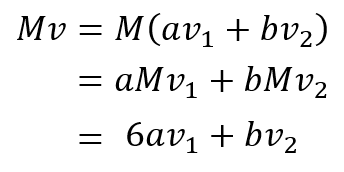
各固有ベクトルの方向にそれぞれ「固有値倍」されています。このように、ベクトルを固有ベクトルで表現することで、行列での変換において単に固有値倍すればよくなり、計算が楽になります。
行列の対角化という言葉を聞いたことがあるかもしれません。詳細は述べませんが、本章で説明したことは行列の対角化の内容に非常に近いものです。詳細が知りたい方や、対角化について昔理解できなかった方は、ぜひ本章の考え方を踏まえた上で調べてみて下さい。
これから固有ベクトルの方向や固有値について理解を深めていきたいと思います。その事前準備として、本章ではまず「二次形式」と呼ばれる関数について説明します。急に関数の話が始まり混乱するかもしれませんが、大事な前提知識となりますので、しっかりと理解して頂きたいと思います。
まずは1変数の二次関数について復習しましょう。例を挙げると次のような式になります。
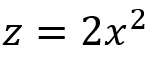
この関数では x に数値を代入することで z が計算されます。この x のように数値を代入される入れ物を変数と呼びます。この二次関数を可視化すると次のようになります。
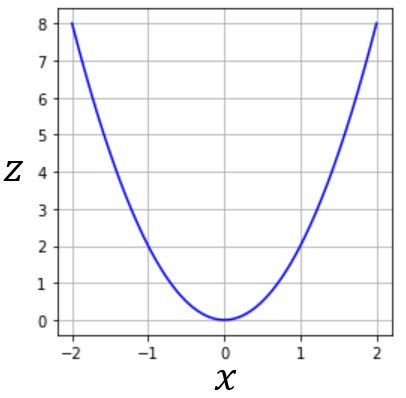
本記事では、ここまで x と y を含む2次元ベクトルを扱ってきました。そこで、 x と y の2変数を含む二次関数について考えてみましょう。まずは次の式を見てみましょう。
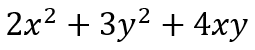
1変数 (x のみ) の二次関数と比較すると y を含む項が増えています。特に着目すべき点として x と y を掛け合わせた項 (上の例では 4xy) が含まれています。上の式には x 同士や y 同士、または x と y の積を取った項のみ含まれており、x や y 単体の項 (例えば 3x や 6y など) が含まれていません。このような x 2や xy の項 を二次の項と呼び、二次の項のみで構成された二次関数を「二次形式」と呼びます。関数の視点から見ると、本記事の説明範囲では二次形式が重要となるため、これ以降は二次関数として二次形式に限定して話を進めます。
式だけを眺めてもイメージを掴みづらいと思いますので、二次形式の関数を可視化してみましょう。
まずは x と y の積を含まない場合として、以下の式を可視化してみます。
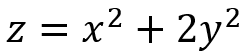
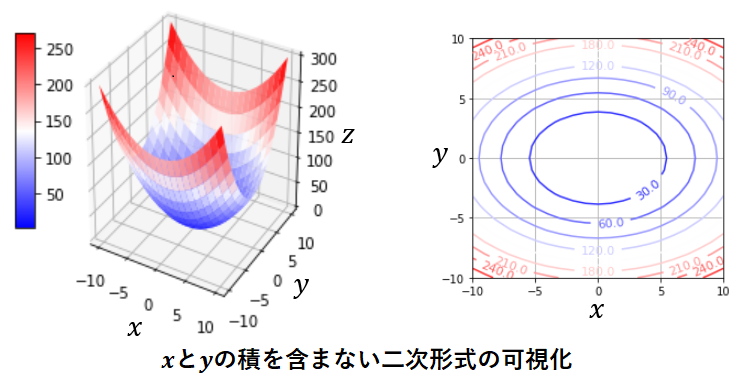
上図左は縦と横に x と y 軸、高さ方向に z 軸を設定してします。上図右は z の値を等高線として表現しています。等高線の方がわかりやすいかもしれませんが、関数の等高線の形状が楕円形であり、楕円の軸が x 軸と y 軸に平行になっています。
次に、 x と y の積を含む場合について確認します。次の式を可視化してみましょう。
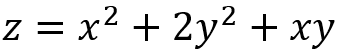
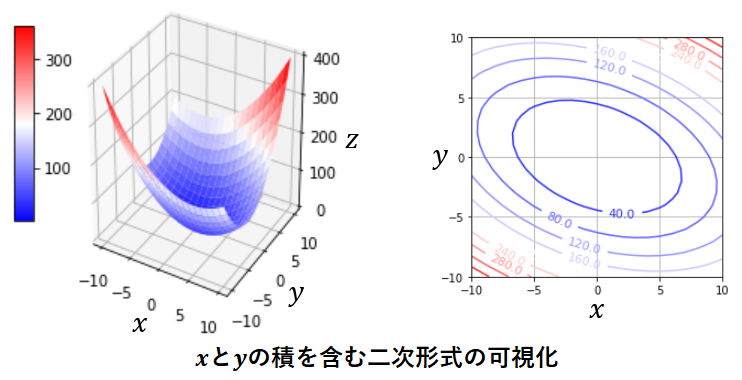
x と y の積の項が含まれると、等高線の楕円の軸が x 軸や y 軸と平行ではなくなることがわかります。
前章では、二次形式と呼ばれる関数の話をしました。本章では、前章の内容を行列の話と繋げていきたいと思います。さっそくですが、既に登場した行列 M とベクトルを使って次の計算を行ってみます。
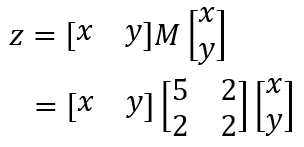
今まで使ってきたベクトルは x と y を縦に並べたものでしたが、上式には x と y を横に並べたベクトルが含まれています。このベクトルを1行2列の行列と捉えることで、先に説明した行列の計算ルールを適用することができます。計算を進めてみます。
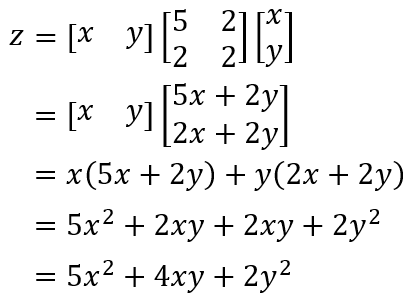
結果として二次形式の関数が出てきました。またこの計算を逆に辿ることで、二次形式の関数について行列を使った形式で表すことができます。
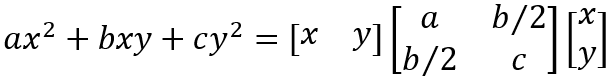
上の変換式から、二次形式の関数を行列で表す場合、行列を対称行列とすることができるとわかります。対称行列ではない行列で表現することもできますが、数学的に都合の良い特性を持っていることから対称行列を使う方が望ましいでしょう。
前章までの説明で、二次形式の関数と行列の関係について理解頂けたかと思います。事前知識の整理ができましたので、ようやく固有ベクトルの向きや固有値について、その特性を見ていきたいと思います。
改めて、既に登場した行列 M を使って次のように二次形式の関数を計算します。
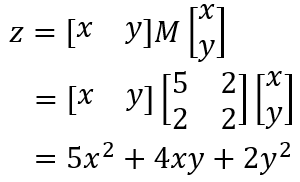
得られた二次形式の関数を可視化してみましょう。そして等高線のグラフに、行列 M の固有ベクトルを重ねて表示します。見やすさのために固有ベクトルの長さは調整しており、各固有ベクトルの固有値を数字で記載しています。
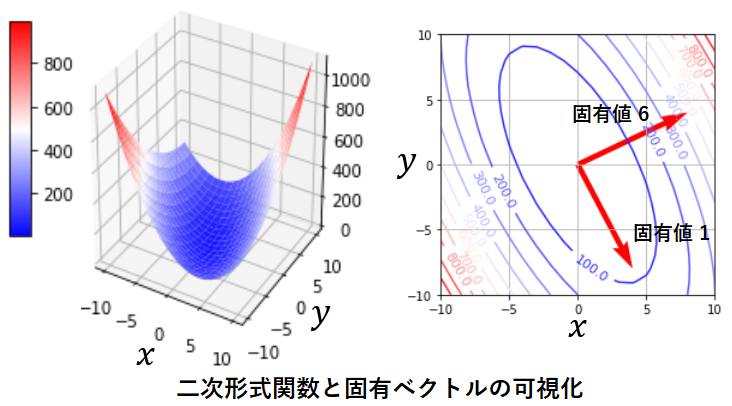
関数の等高線の楕円の軸に対して2つの固有ベクトルが平行であることがわかります。このように、対称行列の固有ベクトルは、その行列から計算される二次形式関数の楕円の各軸に平行になる性質があるのです。さらに固有値は、固有ベクトルの方向に対する関数の「変化の大きさ」を表しています。本記事では数学的な厳密性よりわかりやすさに重点を置いているためこのような表現としますが、固有値が大きな方向には、関数の値がはやく大きくなります。
前章までで、本記事で説明を目指した行列に関する数学的な内容は完了となります。行列に含まれている情報の数学的な意味について少しでも面白さを感じて頂ければ嬉しく思います。数学的な考察だけでも面白いですが、せっかくなので応用例についても少し触れておきたいと思います。本記事で説明した内容は、既にお気付きの方もいるかもしれませんが、主成分分析 (principal component analysis: PCA) が代表的な応用例になります。前章までに登場した関数の、等高線の楕円軸の方向は、そこに含まれている情報の観点において重要な方向であると考えられます。その方向を見つけて、軸を変換することで重要な情報を取り出しやすくしよう、というものが主成分分析の概要となります。本記事では詳細は述べませんが、当社のメンバーが執筆した以下の記事に概要が記載されていますので、ぜひご覧になってください。
【参照 : Azure ML デザイナー を使って、時系列データの異常検知を実践する】
>
https://www.softbanktech.co.jp/special/blog/dx_station/2022/0030/
本記事では、ベクトルや行列の基本的な説明から始めて、行列から計算される二次形式の関数と、固有ベクトルや固有値の関係について解説しました。データ分析に関する数学の面白さが少しでも伝われば幸いです。
当社では AI や機械学習を活用するための支援を行っております。持っているデータを活用したい、AI を使ってみたいけど何をすればよいかわからない、やりたいことのイメージはあるけれどどのようなデータを取得すればよいか判断できないなど、データ活用に関することであればまず一度ご相談ください。一緒に何をするべきか検討するところからサポート致します。データは種類も様々で解決したい課題も様々ですが、イメージの一助として AI が活用できる可能性のあるケースを以下に挙げてみます。
上記は一例となりますがデータ活用に関して何かしらの課題を感じておりましたら、当社までお気軽にお問い合わせください。
関連ページ |